what do alternate interior angles add up to
Alternate interior angles are the angles formed when a transversal intersects two coplanar lines. They lie on the inner side of the parallel lines just on the opposite sides of the transversal. The transversal crosses through the two lines which are Coplanar at carve up points. These angles represent whether the 2 given lines are parallel to each other or non. If these angles are equal to each other and then the lines crossed by the transversal are parallel.In this article, we will discuss what are alternate interior angles, the theorem statements and proofs based on the alternate interior angles, what is a co-interior bending, and many solved examples.
Tabular array of Contents:
- What is an Alternate Interior Bending?
- Backdrop
- Theorems and Proofs
- Antithesis of the Theorem
- Co-interior Angles
- Co-interior Angle Theorem and Proof
- Solved Examples
- FAQs
Alternating Interior Angles Definition
The angles which are formed within the two parallel lines, when intersected past a transversal, are equal to its alternate pairs. These angles are chosen alternate interior angles.

In the above-given figure, you can see, two parallel lines are intersected by a transversal. Therefore, the alternate angles inside the parallel lines will exist equal.
i,eastward. ∠A = ∠D and ∠B = ∠C
Properties
- These angles are coinciding.
- The sum of the angles formed on the same side of the transversal which are within the two parallel lines is always equal to 180°.
- In the case of not – parallel lines, alternating interior angles don't have whatsoever specific properties.
- Adjacent Angles Vertical
- Corresponding Angles
- Complementary Angles Supplementary Angles
- Parallel Lines Transversals Bending
- Lines And Angles Class seven
- Lines And Angles Class 9
Theorem and Proof
Statement: The theorem states that " if a transversal crosses the gear up of parallel lines, the alternate interior angles are coinciding".
Given: a//d
To testify: ∠four = ∠v and ∠3 = ∠six
Proof: Suppose a and d are two parallel lines and l is the transversal that intersects a and d at points P and Q. See the effigy given below.
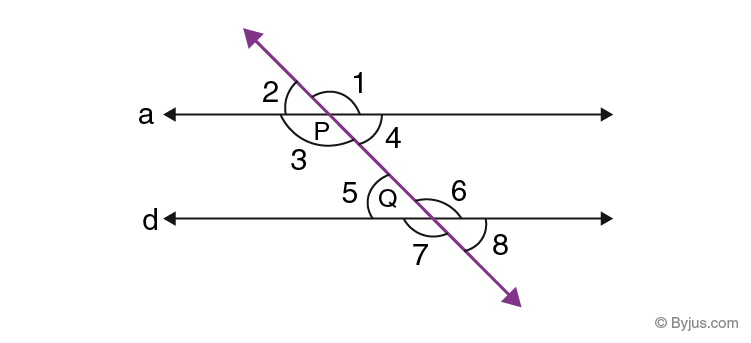
From the backdrop of the parallel line, nosotros know if a transversal cuts any 2 parallel lines, the corresponding angles and vertically opposite angles are equal to each other. Therefore,
∠ii = ∠5 ………..(i) [Corresponding angles]
∠2 = ∠4 ………..(ii) [Vertically contrary angles]
From eq.(i) and (two), we go;
∠4 = ∠5 [Alternate interior angles]
Similarly,
∠three = ∠six
Hence, it is proved.
Antithesis of Theorem
If the alternate interior angles produced by the transversal line on two coplanar are coinciding, then the two lines are parallel to each other.
Given: ∠4 = ∠5 and ∠3 = ∠6
To prove: a//b
Proof: Since ∠2 = ∠iv [Vertically opposite angles]
So, we can write,
∠ii = ∠5, which are respective angles.
Therefore, a is parallel to b.
Co-interior Angles
Co-interior angles or Sequent interior angles are the two angles that are on the aforementioned side of the transversal. Co-interior angles are the interior angles and it sums up to 180 degrees. It means that the sum of two interior angles, which are on the same side of transversal is supplementary. Co-interior angles resemble like in "C" shape and both the angles are not equal to each other. The co-interior bending is as well known as the consecutive interior angles or the same side interior angles.
Co-interior Angle Theorem and Proof
Statement:
If the transversal intersects the two parallel lines, each pair of co-interior angles sums up to 180 degrees (supplementary angles).
Proof:

Allow us consider the image given to a higher place:
In the effigy, angles 3 and 5 are the co interior angles and angles four and 6 are the co-interior angles.
To prove: ∠3 and ∠5 are supplementary and ∠iv and ∠6 are supplementary.
Given that, a and b are parallel to each other and t is the transversal.
By the definition of linear pair,
∠1 and ∠3 forms the linear pair.
Similarly, ∠ii and ∠4 form the linear pair.
Past using the supplement postulate,
∠i and ∠iii are supplementary
(i.due east.) ∠1 + ∠iii = 180
Similarly,
∠ii and ∠4 are supplementary
(i.e.) ∠two + ∠4 = 180
By using the corresponding angles theorem, we can write
∠ane ≅∠v and ∠2 ≅ ∠6
Thus, by using the exchange property, nosotros can say,
∠iii and ∠five are supplementary and ∠4 and ∠half dozen are supplementary.
Hence, the co-interior angle theorem (consecutive interior angle) is proved.
The converse of this theorem is "if a transversal intersects ii lines, such that the pair of co-interior angles are supplementary, then the 2 lines are parallel".
Facts about sequent interior or co-interior angles:
- Consecutive interior or co-interior angles contains different vertices but lie on the same side of the transversal
- These angles lie between two lines
- Consecutive interior angles are non-adjacent angles
- If a transversal is drawn on two parallel lines, so the sum of co-interior angles formed are e'er added upwardly to 180 degrees
- The sum of sequent interior angles of a parallelogram is e'er supplementary
Examples
Question 1:
Find the value of B and D in the given figure.
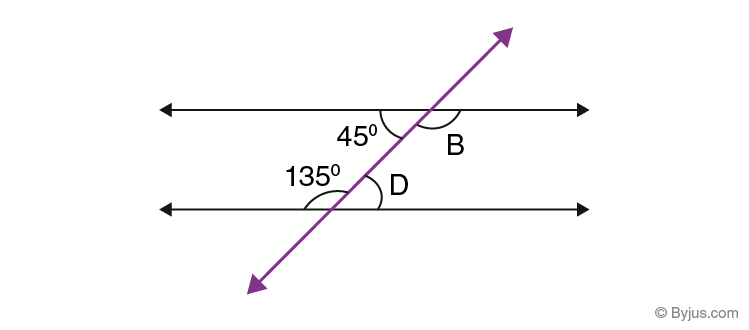
Solution:
Since 45° and D are alternate interior angles, they are congruent.
So, D = 45°
Since 135° and B are alternate interior angles, they are congruent.
So, B = 135°
Question ii:
Detect the missing angles A, C and D in the following effigy.
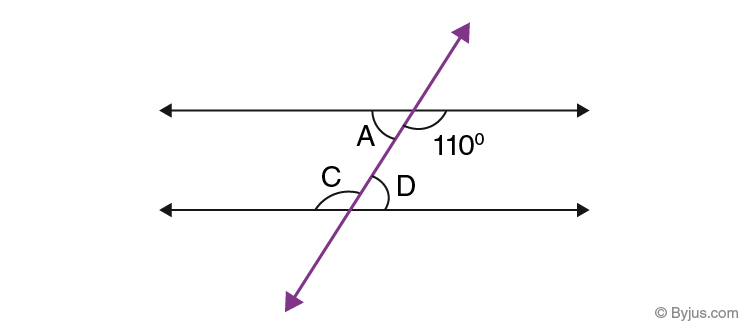
Solution:
As angles ∠A, 110°, ∠C and ∠D are all alternate interior angles, therefore;
∠C = 110°
By supplementary angles theorem, nosotros know;
∠C+∠D = 180°
∠D = 180° – ∠C = 180° – 110° = lxx°
Example iii:
Discover the value of 10 from the given below figure.

Solution:
Nosotros know that alternating interior angles are congruent.
Therefore, 4x – 19 = 3x + xvi
4x – 3x = 19+16
x = 35
Since,
∠A = ∠D
Therefore, ∠A = 70°.
Download the BYJU'Southward App and become a better learning feel with the help of personalised videos.
Oft Asked Questions on Alternate Interior Angles
What is meant by alternating interior angles?
The alternate interior angles are the angles that are formed inside the two parallel lines, when it is intersected by a transversal, and are equal to its alternate pairs.
What is meant by co-interior angle?
The co-interior angle, also known as the consecutive interior angle, if the transversal intersects the ii parallel lines, each pair of co-interior angles sums up to 180 degrees (supplementary angles)
What is the antipodal of the alternate interior angle theorem?
The converse of alternate interior angle theorem states that "If the alternate interior angles produced by the transversal line on two coplanar are coinciding, and so the two lines are parallel to each other"
Mention the properties of alternate interior angles.
The alternate interior angles are congruent.
The consecutive interior angles are supplementary.
Does the co-interior bending are supplementary, if the transversal intersects the parallel line?
Yes, the co-interior angles are supplementary when the transversal intersects the parallel line.
Source: https://byjus.com/maths/alternate-interior-angles/
0 Response to "what do alternate interior angles add up to"
Post a Comment